3º jueves 29 octubre

FACTORIZACIÓN:

Tarea:

No hay tarea.

1º jueves 28 octubre

Actividad de clase:

Escribir el espacio muestral de algunos eventos en su libro de texto de la deportista.
Atender a una presentación sobre diagrama rectangular y diagrama de árbol.
Realizar apunte de diagrama rectangular:

DIAGRAMA RECTANGULAR Y DIAGRAMA DE ÁRBOL.

Para organizar la información se puede presentar mediante dos arreglos: diagrama rectangular y de árbol.

DIAGRAMA RECTANGULAR.

Se usa cuando el evento está formado por dos variables.

En el eje horizontal se marca una variable y en el eje vertical la otra variable.

Cada punto de cruce del rectángulo representa una solución del evento.

Para escribirse cada solución se utilizan paréntesis separados por comas.

Ejemplos:

Se tiran 2 dados, hacer el diagrama rectangular:

Ejercicio en su cuaderno:

Realizar los diagramas rectangulares de su libro de la deportista páginas 74 y 75.

Tarea:

Realizar el acertijo de su libro de la antena página 50 y hacer en grande, los problemas de la tarea de la clase anterior.

2º jueves 29 octubre

SUMA Y RESTA DE ÁNGULOS
Recordando:
1º = 60'
1' = 60''

La suma y resta de ángulos se realiza de manera semejante que las sumas y restas con el tiempo.
Ejemplos:
(32º 16' 36'') + (45º 12' 04'') = 77º 28' 40''

(15º 28' 42'') + (74º 30' 25'') = 89º 58' 67''
como 67 segundos equivale a 1 minuto y 7 segundos, el resultado será:
89º 59' 07''

(75º 15' 49'') - (34º 10' 35'') = 41º 05' 14''
(96º 12' 05'') - (15º 37' 02'') = al hacer la resta a 12 minutos no le puedo restar 37 minutos, por lo que los minutos le piden 1 a los grados, solamente que recordemos que 1 grado equivale a 60 minutos.
(95º 72' 05'') - (15º 37' 02'') = 80º 35' 03''

Ejercicio:
Resolver el ejercicio del libro azul página 71.

Tarea:
Terminar el ejercicio azul, más los ejercicios pendientes de sus libros.

1º martes 27 octubre

PROBLEMAS DE PROPORCIONALIDAD

1. Tres amigos obtienen un premio de $1000 en la lotería. ¿Cómo deben repartírselo según lo que gastó cada uno si uno de ellos puso $12.00, el otro $8.00 y el tercero $15.00?

Este problema es de proporcionalidad directa, porque quien aportó más para la compra del boleto debe recibir más por la repartición del premio. La proporcionalidad directa se resuelve por productos cruzados.

1. Supongan ahora que el premio es de $1500.00 Si uno de ellos aportó una séptima parte del costo del billete y los otros dos amigos, el resto en partes iguales, ¿qué cantidad le corresponde a cada uno si reparten el premio proporcionalmente?

Este problema también es de proporcionalidad directa, ya que quien aporta más para el costo del billete, debe recibir más también de la repartición del premio.

Si el amigo uno aportó la séptima parte del costo del billete, haciendo un diagrama, los dos amigos restantes que aportaron lo mismo aportaron cada uno 3/7 partes del costo del billete.

Ejercicio:

Resolver en grupo las páginas 43, 44 y 45 de su libro de la antena.

Tarea:

Resolver por sorteo los problemas que les toque de su libro de la deportista páginas 70 y 71 y escribirlo en su papelote con su solución y explicación.

2º martes 27 octubre

PARES DE ÁNGULOS
Trazo de ángulos con transportador:

Copiar los ángulos anteriores usando regla y compás:

Pasos

1º Se traza una línea, mas o menos igual al ángulo que se va a copiar.

2º Se traza un arco que cruce al ángulo y de la misma medida otro arco en la línea del ángulo que se va a copiar.

3º Se toma la medida con el compás del arco en sus cruces y con la misma medida se marca en el ángulo que se está copiando.

CONVERSIONES DE ÁNGULOS

La unidad de medida de los ángulos es el grado.

Los grados se dividen en minutos, y los minutos se dividen en segundos.

1º = 60' (un grado = 60 minutos)

1' = 60'' (un minuto = 60 segundos)

1º = 3600'' (un grado = 3600 segundos)

Ejercicio 1:

Resolver en el libro naranja las páginas 36, 37 y 38

Ejercicio 2:

Resolver en el libro azul la página 70.

Tarea:

Resolver en el libro naranja las páginas 39 y 40.

3º lunes 26 de octubre

FACTORIZACIÓN DE TRINOMIOS DE LA FORMA x2 + bx + c.




Es el resultado de los binomios con término común.



Ejemplos de trinomios de la forma x2 + bx + c:
Características:

1. Siempre son 3 términos.


2. Empieza con x2 (a2, b2, ...)
   

Pasos:

1. Sacar raíz del primer término y escribirla en los dos paréntesis.


2. Se copia el signo del 2º término y se escribe en el primer paréntesis.


3. Se multiplican los signos del 2º y 3º términos y se escribe en el segundo paréntesis.


4. Se buscan dos números que sumados o restados den el 2º número y multiplicados den el 3º número. (Adivinanza) El número mayor se escribe en el primer paréntesis.

Tarea:
Aplicar esta factorización en los trinomios de su libro morado páginas 55 y 56. Y en su libro naranja páginas 29 y 30.

2º lunes 26 octubre

ANGULOS

Definición de ángulo: abertura entre dos rayos o semirrectas que tienen un vértice en común.

Un ángulo se define como:

Tipos de ángulos:

Actividad de clase: analizar presentación sobre modelos geométricos.

Ejercicio y tarea:

Resolver en el libro naranja ejercicios de modelos geométricos y sobre ángulos, de la página 29 a la 35.

1º viernes 23 octubre

Ver presentación relativa al tema de proporcionalidad.

PROPORCIONALIDAD INVERSA

Problema: Se encargaron pizzas para una fiesta, calculando que 15 personas la consuman en 30 minutos; si a la fiesta asisten 25 personas, ¿en cuánto tiempo se acabará la pizza?

a) ¿y si van 10 personas?

b) ¿y si van 5 personas?
c) ¿y si van 30 personas?

Gráfica:

Definición de proporcionalidad inversa: es la relación donde a medida que aumenta una cantidad la otra disminuye.

Las proporciones inversas se resuelven como una multiplicación de fracciones:

Gráficamente una proporción inversa será una curva llamada hipérbola.

Ejercicios en hoja para entregar:

1. Una pared la construyen 8 albañiles en 5 días, ¿en cuánto tiempo la construirán 10 albañiles?
   
2. Una herencia se reparte entre 15 personas y les toca de $300,000 a cada una. Si la herencia se reparte entre 50 personas de cuánto les toca, y si se reparte entre 10 personas?


3. Inventar y resolver por binas una problema de proporcionalidad inversa.

Ejercicio en su libro de texto de la deportista:

Resolver los problemas de su libro de texto página 68.

Tarea:

Inventar y resolver dos problemas de proporcionalidad directa.

1º jueves 22 de octubre

PROPORCIONALIDAD DIRECTA

Problema:

Si una vela de 25 cm de altura dura encendida 50 horas, ¿cuánto tiempo duraría encendida otra vela del mismo grosor, de 12 cm de altura?

a) ¿cuánto duraría una vela de 1 cm?

b) ¿cuánto duraría una vela de 10 cm?

c) ¿cuál sería la medida que debe tener una vela para que dure 30 horas?

Gráfica:

Proporcionalidad directa: es la relación donde a medida que aumenta una variable, la otra variable aumenta también.

Las proporciones directas se resuelven por regla de tres (productos cruzados)

Gráficamente una proporción directa se ve como una línea recta.

Ejercicio:

1. Si se compran 12 chocolates con $30, ¿cuántos chocolates se comprarán con $100?
   
2. Si trabajo 8 horas ganaré $160, ¿cuánto ganaré en 30 horas?
   

Resolver en hoja para entregar la siguientes proporciones:

Ejercicio en el libro de la antena:

páginas 40 - 41

Tarea:

Resolver en el libro de la deportista trazos de simetría axial en las páginas 58 y 59.

Resolver en el libro de la antena los problemas de proporcionalidad página 42.

2º jueves 22 de octubre

MODELOS GEOMÉTRICOS

Definición: Es utilizar áreas para obtener resultados de multiplicaciones.


Ejemplos:

Ejercicio:

Libro azul página 60

Tarea:

Resolver las páginas 29, 30, 31 y 32 del libro naranja.

1º martes 20 de octubre

SIMETRÍA AXIAL

Simetría axial: es un procedimiento para trazar figuras iguales a través de una línea llamada eje.

Ejercicio:

Trazar figuras simétricas en su libro de texto de la antena páginas 36, 37, 38 y 39

Tarea.

En media cartulina, pegar 5 figuras que tengan eje de simetría, y trazar en cada una el eje de simetría.

2º martes 20 octubre

SIMPLIFICACIÓN DE TÉRMINOS SEMEJANTES.

Encierra con el mismo color los términos semejantes

Definición de términos semejantes: son los que tienen la misma parte literal (las mismas letras con los mismos exponentes).

Acomodar los términos semejantes y reducirlos.

Ejercicio:

Reducir los términos semejantes:

Tarea:

Reducir los términos semejantes en su libro azul página 57.

3º miércoles 14 de octubre

FACTORIZACIÓN DE DIFERENCIA DE CUADRADOS:

Llamamos diferencia de cuadrados al resultado de los binomios conjugados.

Ejemplos de diferencias de cuadrados:

Características:

- Son siempre dos términos.

- Uno es positivo y el otro negativo.

- Los dos términos tienen raíz cuadrada exacta.

Pasos:

1. Se abren dos paréntesis.

2. Se escriben en los dos paréntesis las raíces, en un paréntesis va una suma y en el otro paréntesis va una resta.

Ejercicio 1:

Libro morado página 52

Ejercicio 2:

Libro naranja páginas 30 - 33.

FACTORIZACIÓN DE TRINOMIOS DE LA FORMA X2 + bx + c.

Ejemplos:

1º martes 13 de octubre

TRAZOS

1) Trazo de rectas paralelas con escuadras:

Ejercicio:

Libro deportista página 54

2) Trazo de rectas perpendiculares con escuadras:

Ejercicio:

Libro deportista página 55

3) Trazo de rectas perpendiculares con compás:

Ejercicio:

Libro deportista página 57

Ejercicio:

Realizar en una hoja blanca un cubo con rectas paralelas y perpendiculares, decorado y coloreado.

2º martes 13 octubre

Ejercicio 1:

Revisar ejemplos de lenguaje algebraico en su libro azul pp. 108 - 110.

Ejercicio 2:

Resolver dudas de tarea del libro naranja páginas 21 y 22.

Ejercicio 3:

Hacer ejercicios de repaso a examen:

1º viernes 9 de octubre

Ejercicio 1:
Resolver ejercicios de repaso a examen.

TRAZO DE RECTAS PARALELAS Y PERPENDICULARES.

Lectura en su libro de la deportista y subrayar las respuestas.

Pasar las preguntas en su cuaderno y contestarlas.

1. ¿Qué es una transformación geométrica?
2. Tipos de transformaciones y explicación de cada uno.
3. Tipos de isometrías.
4. ¿Cómo se nombra un punto?
5. ¿Cómo se nombra una recta?
6. ¿Cómo se nombra un segmento?
7. ¿Cómo se nombra una semirrecta o rayo?
8. ¿Qué son líneas paralelas?
9. Símbolo de las rectas paralelas.
10. ¿Qué son líneas perpendiculares?
11. Símbolo de las rectas perpendiculares.

Tarea:

Resolver los ejercicios de repaso a examen.

3º viernes 9 de octubre

REPASO

Resolver los ejercicios de repaso a examen dados en fotocopia.

FACTORIZACIÓN DE TRINOMIO CUADRADO PERFECTO

Llamamos trinomio cuadrado perfecto al resultado del binomio al cuadrado.

Características:

• 
  
  Son tres términos
• 
  
  El 1º y el 3º tienen raíz cuadrada exacta y son positivos.
• 
  
  El 2º término es el doble de las raíces.

Pasos:

1. 
   
   Se sacan las raíces del 1º y el 3º términos, con el signo del segundo término
2. 
   
   Se escriben dentro de un paréntesis y se eleva al cuadrado.
   

Ejemplos:

Ejercicio 2:

Libro morado páginas 52 y 53

Ejercicio 3:

Libro naranja páginas 30 y 31

Tarea:

Hacer ejercicio de repaso a examen.

1º jueves 8 de octubre

PERÍMETRO DE FIGURAS.

Perímetro: es la medida de alrededor de una figura. Se obtiene sumando las medidas de sus lados.

Ejercicio 1:

Pegar las figuras dadas en fotocopias y calcular su perímetro dando las medidas de sus lados.

Ejercicio 2:

Contestar su libro de la antena páginas 34, 35.

Tarea:

Calcular el perímetro de las figuras en su libro de la deportista página 44 y contestar la evaluación en su libro páginas 47 y 48.

2º jueves 8 de octubre

Ejercicio 1:
Libro naranja páginas 19 y 20. Resolver ecuaciones sencillas de primer grado.

LENGUAJE ALGEBRAICO

Definición: es escribir con símbolos una expresión con palabras.

Ejemplos:

x es un número cualquiera

x/2 es la mitad de un número

2x es el doble de un número

x2 es el cuadrado de un número

x + 2 es un número aumentado en 2

x - 2 es un número disminuido en 2

x/3 es la tercera parte de un número

3x es el triple de un número

x3 es el cubo de un número

x + 3 es un número aumentado en 3

x + y es la suma de dos números

x/y es el cociente de dos números

xy es el producto de dos números

x - y es la diferencia de dos números

x + x + 1 es la suma de dos números consecutivos

(x + y)/2 es la semisuma de dos números

Ejercicio 2:

Libro azul páginas 108 - 110.

Tarea:

Libro naranja páginas 21 y 22.

3º miércoles 7 de octubre

FACTORIZACIÓN

a) FACTORIZACIÓN POR FACTOR COMÚN.

Factorización: proceso recíproco de los productos notables. Es dado un resultado definir su multiplicación.

Factorizar los polinomios siguientes aplicando la propiedad distributiva, ejemplos:

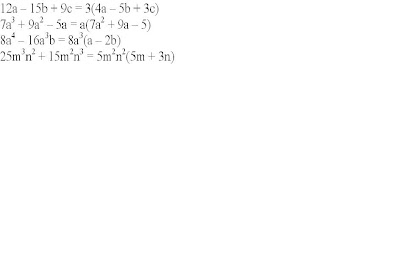Características:

- En esta factorización siempre hay un divisor común numérico y/o una letra repetida en todos los términos.

Pasos:

1) Se busca el máximo común divisor de los términos:

• 
  
  Con los coeficientes o números se busca un divisor común de todos los téminos, el mayor posible.

• 
  
  Con las variables o letras se busca la leatra repetida y si tienen exponente se busca el menor de ellos.

2) Se divide cada término entre el factor común que es el máximo común divisor y se escribe en un paréntesis.

Ejercicio 1:

Libro naranja actividad 1.17, actividad 1.18, actividad 1.19, páginas 25, 26 y 27.

Ejercicio 2:

Libro morado páginas 49 y 50.

Ejercicio 3 en cuaderno:

Tarea:
Actividad 1.20 libro naranja página 28.

1º martes 6 de octubre

VARIABLES Y CONSTANTES.

Variable: Son símbolos que pueden tener cualquier valor. (son letras)

Constantes: Son símbolos cuyo valor no cambia. (constantes)

Ejercicio:

En las siguientes fórmulas separar las variables de las constantes:

Ejercicio:

Libro de la antena páginas 32, 33 y 34

Tarea:

Resolver un problema de lógica:

Una estos nueve puntos con 4 líneas rectas, sin levantar el lapiz del papel ni pasar dos veces por el mismo sitio.

2º martes 6 de octubre

ECUACIONES SIMPLES

Adivinanzas:

Adivina el número que estoy pensando:

a) "Si lo multiplico por 3 y le resto 2 obtengo 43. ¿Cuál es el número?"

b) "Si lo diviido entre 2 y le sumo 4 obtengo 10. ¿Cuál es el número?"

Ecuación: Es una igualdad que tiene alguna incógnita.

Resolver una ecuación: Es encontrar el valor de la incógnita que hace verdadera la igualdad.

Propiedad fundamental de la igualdad:

"Si a un miembro de la igualdad se le suma o se le resta un número, al otro miembro de la igualdad se le debe sumar el mismo número."

Ejemplo:

x + 3 = 9

x + 3 - 3 = 9 - 3

x = 6

x - 4 = 10

x - 4 + 4 = 10 + 4

x = 14

"Si a un miembro de la igualdad se le multiplica o se le divide por un número, al otro miembro de la igualdad se le deber multiplicar o dividir por el mismo número."

Ejemplo:

4x = 24

(4x)/4 = 24/4

x = 6

x/3 = 2

(3) x/3 = 2 (3)

x = 6

Ejercicio en el cuaderno:

Resuelve las siguientes ecuaciones simples.

3x + 2 = 8

4x - 1 = -9

6x + 2 = -10

Tarea:

Resolver en hoja para entregar las siguientes ecuaciones simples:

• x + 9 = 11
• 2x - 5 = 7
• 3x + 1 = 16
• 6x = -30

3º lunes 5 de octubre

REPASO DE BINOMIOS NUMÉRICOS

Unir con líneas el producto notable con su solución:

Ejemplos de productos numéricos:

42 x 42 = (40 + 2)2 = 1600 + 160 + 4 = 1764

57 x 63 = (60 - 3) (60 + 3) = 3600 - 9 = 3591

92 x 96 = (90 + 2) (90 + 6) = 8100 + 720 + 12 = 8832

22 x 22 x 22 = (20 + 2)3 = 8000 + 2400 + 240 + 8 = 82648

Ejercicio y tarea:
Libro morado páginas 46 y 47.

2º lunes 5 de octubre

OPERACIONES DE NÚMEROS CON SIGNO.

PROBLEMAS

a) Si una persona tiene 8 pesos y debe 11 pesos, ¿cuál es su situación económica?

8 - 11 = -3

Debe 3 pesos

b) Una persona nació en el año 123 a.c. y vivió 65 años. ¿En qué año murió?

- 123 + 65 = -58

Murió en el año 58 antes de cristo.

a) SUMA

Ley de los signos: Signos iguales se suman, signos diferentes se restan, y queda el signo de mayor valor absoluto.

Ejemplos:

a) 3 + 9 - 5 - 4 = 12 - 9 = 3

b) - 5 + 6 - 7 + 1 + 3 = 10 - 12 = -2

c) (+3) + (-5) + (-6) = +3 - 5 - 6 = 3 - 11 = -8

b) RESTA

La ley de los signos es la misma que la de la suma y resta.

En la resta encontramos paréntesis inversos. El inverso de + es -, el inverso de - es +

Ejemplos:

a) (+3) - (- 5) = 3 + 5 = 8

b) (- 3 ) - ( - 4 ) = - 3 + 4 = 1

c) (+ 4 ) + ( - 2 ) - ( + 6 ) - ( - 3 ) = + 4 - 2 - 6 + 3 = 7 - 8 = - 1

c) MULTIPLICACIÓN

Ley de los signos:

( + ) ( + ) = +

( + ) ( - ) = -

( - ) ( + ) = -

( - ) ( - ) = +

Si son varios factores, sólo me fijo en los signos -, y los cuento, si ese número es para el resultado es positivo, si ese número es impar el resultado es negativo.

Ejemplos:

a) ( + 3 ) ( - 2 ) = - 6

b) ( - 3 ) ( - 4 ) ( + 2 ) ( - 1 ) = - 24

c) ( + 2 ) ( - 3) + ( - 3 ) ( - 5 ) = - 6 + 15 = 9

d) DIVISIÓN

La ley de los signos es la misma que la de la multiplicación.

Ejemplos:

a) ( + 6 ) : ( - 3 ) = - 2

b) ( - 12 ) : ( - 6 ) = + 2

c) ( - 5 - 7 ) : ( - 2 ) = ( - 12 ) : ( - 2 ) = + 6

Ejercicio:

Libro azul páginas de la 48 a la 53.

Tarea:

Libro naranja páginas 18 y 19, actividades 1.5, 1.6, 1.7, 1.8

1º viernes 2 de octubre

SERIES FIGURATIVAS

Ejemplos:

Ejercicio 1:

Libro de la antena páginas 29, 30 y 31

Ejercicio 2:

Libro de la deportista páginas 40 y 41

Tarea:

Realizaar con material como pasta de sopa, bolitas de papel, plastilina, calcomanías, etc. una serie figurativa.

3º viernes 2 de octubre

BINOMIO AL CUBO.
Regla del binomio al cubo:

• cubo del primer término
  
• triple del cuadrado del primer término por el segundo término


• triple del primer término por el cuadrado del segundo término


• cubo del segundo término

Ejemplo:

Ejemplos:

Ejercicio:

Libro morado página 45

Tarea:

Incluir el binomio al cubo en su ficha bibliográfica, después enmicarla o forrarla para usarse en adelante.

3º jueves 1º de octubre

REPASO DE PRODUCTOS NOTABLES:
Consultando su ficha bibliográfica de los productos notables resolver las siguientes tres multiplicaciones notables:

• (x + 3)2
• (x + 3) (x - 3)
• (x + 3) (x - 2)

Observar cómo son diferentes sus soluciones correspondientes:

• x2 + 6x + 9
• x2 - 9
• x2 + x - 6

Resolver los ejercicios de su libro naranja páginas 24 a la 26.

Tarea:

Recortar las figuras del binomio al cubo dadas en fotocopia.

1º jueves 1º de octubre

SERIES NO ARITMÉTICAS.
Series no aritméticas: Son las que no se les suma o resta la misma cantidad, aunque si tienen una regla definida.
Ejemplos:
a) 3, 4, 6, 9, 13, ___, ___, ___ regla: en esta serie se le va sumando a cada número +1, +2, +3, +4, y así progresivamente.

b) 10, 12, 16, 22, ___, ___, ___ regla: en esta serie se le va sumano +2, +4, +6, +8, y así progresivamente.

c) 1, 2, 5, 12, 29, ___, ___, ___ regla: en esta serie se va escribiendo el doble del número anterior más el ante anterior, doble de 1 más cero = 2, doble de 2 más 1 = 5, doble de 5 más 2 = 12, doble de 12 más 5 = 29, y así sucesivamente.

Ejercicio:
Resolver en el libro de la deportista las series no aritméticas de las páginas 38 y 39.
Tarea:
Inventar tres series no aritméticas, que contenga cada una aproximadamente 10 números; expresando la regla de la sucesión.

2º miércoles 1º de octubre

Resolver ejercicios en el libro naranja:
Terminar los ejercicios y problemas hasta la página 17.
En el libro azul:
Terminar y hacer las simplificaciones que faltaron en su libro páginas 42 a 46.
Tarea:
No hay tarea