3º miércoles 14 de abril

TRIÁNGULOS RECTÁNGULOS

Terminar el cálculo de área y perímetro de la clase del lunes.

Ejemplo 2:

Ejercicio libro morado página 191: elegir 3 ejemplos de los triángulos rectángulos y calcular en ellos los datos que se piden.

Tarea:
Resolver en una hoja para entregar un ejercicio de triángulo rectángulo:

1º martes 13 de abril

PROBLEMAS SOBRE PORCENTAJES.

1. Para ir al partido inaugural del mundial, voy a pagarlo en 6 mensualidades. Me van a incrementar el 8% de intereses. Si el boleto cuesta $72 000. ¿Cuánto pagaré cada mes?



2. Quiero comprar una pantalla LCD de 42" y se ofrece con pago al contado en 8,096 pesos; en otra tienda la ofrecen con 12 pagos iguales de $895. ¿Qué porcentaje de diferencia hay en las dos formas de pago?

Actividad de clase:

Se repartieron problemas de su libro de la antena de porcentajes para resolver en clase, tres problemas por alumno. Pueden ayudarse los miembros de un mismo equipo.

Tarea:

Pasar a papelote los problemas realizados en clase, para exponerlos.

2º martes 13 de abril

FUNCIONES LINEALES

Resolver en el libro naranja las páginas 196 - 198.

Forma de la función de primer grado: y = mx + b

donde m es la pendiente e indica la inclinación y b es la ordenada al origen y es el valor inicial.

Ejemplos:

Tabular y graficar las siguientes funciones:

y = 3x - 2

y = - 4x + 1

y = - 1/2 x -2

y = 3/5x + 1

Tarea:

Graficar las funciones en su libro azul páginas 189 y 190.

3º lunes 12 de abril

TRIÁNGULOS RECTÁNGULOS.

Para resolver triángulos rectángulos se necesitan dos datos:

a) un ángulo agulo y un lado.

b) dos lados

Teniendo los datos podemos calcular los demás lados del triángulo utilizando trigonometría y teorema de Pitágoras.

Ejemplo 1:

2º lunes 12 de abril

TESELACIÓN

Consultar en internet los siguientes videos:

http://www.youtube.com/watch?v=eltOhzcts_g

http://www.youtube.com/watch?v=1SxNcYO6X5k

Definición de teselación: es una composición que se utiliza para cubrir el plano utilizando figuras.

Escher fue un litógrafo que hacía representaciones creativas con motivos ornamentales.

Para construir teselaciones podemos usar figura como triángulos equiláteros, cuadrados o polígonos regulares.

El procedimiento se basa en eliminar una parte de uno de los lados del polígono para agregársela al lado contrario. Esta acción se repite hasta obtener la figura deseada.

Ejemplo:

Ejercicio de clase:

Realizar la teselación de una figura y hacer en la hoja impresa el mosaico formado.

1º martes 9 de marzo

Actividad de clase:
Resolver a través de una presentación los problemas sobre cuadriláteros en su libro naranja páginas 163 - 168.

Tarea:
No hay tarea.

2º martes 9 de marzo

FÓRMULA DEL ÁNGULO CENTRAL DE UN POLÍGONO REGULAR

Definición: Llamamos ángulo central al que tiene su vértice en el centro del polígono y sus lados llegan a los vértices del polígono.

FÓRMULA DEL ÁNGULO INTERIOR DE UN POLÍGONO REGULAR

Definición: Llamamos ángulo interior al que se forma con dos lados de un polígono regular.

Actividad de clase:

Completar el cuadro siguiente utilizando las fórmulas vistas en clase.

PASOS PARA TRAZAR UN POLÍGONO REGULAR:

1. Trazar una circunferencia de 3 cm de radio.
2. Trazar un radio.
3. Dividir 360º entre el número de lados y marcar el ángulo central de esa medida.
4. Trazar otro radio que pase por la marca de la medida del ángulo.
5. Medir la amplitud del ángulo con el compás y repetir la medida en la circunferencia.
6. Cerrar la figura y recortarla.

Tarea:

Trazar en hojas de colores un triángulo equilátero, un cuadrado, un pentágono regular, un hexágono regular, heptágono regular y octágono regular; siguiendo los pasos escritos en el cuaderno.

2º lunes 8 de marzo

Actividad de clase: terminar cuadro de la clase anterior.

1) Dividir las figuras en triángulos trazando diagonales.

2) Contar las diagonales y contar los triángulos.

3) Deducir la fórmula para el número de de diagonales desde un solo vértice.

(n - 3)

4) Deducir la fórmula para el número de triángulos.

(n - 2)

5) Deducir la fórmula para la suma de los ángulos interiores de un polígono.

(n - 2)(180º)

6) Deducir la fórmula para el número total de diagonales.

(n)(n - 3)/2

Ejercicio:

Contestar por parejas las páginas de su libro naranja:184, 185, 187, 188, 189 y 190.

Tarea:

Resolver las páginas de su libro azul páginas 178 y 179.

1º viernes 5 de marzo

ÁREAS Y PERÍMETROS DE TRIÁNGULOS, ROMBOIDES Y TRAPECIOS.

Realizar un cuadro de repaso de las fórmulas de áreas y perímetros de las siguientes figuras:

Calcular las áreas y perímetros en su libro de la deportista páginas 201 y 202

Resolver por parejas los problemas de su libro de la antena páginas 160 - 163.

Tarea:

Terminar de resolver los problemas en su libro de la antena.

3º viernes 5 de marzo

Actividad de clase:
Resolver un ejercicio en hoja para entregar para aplicar las funciones trigonométricas estudiadas de tarea.
Resolver el ejercicio de su libro naranja páginas 263 a 265.

Tarea:
Resolver las funciones trigonométricas en su libro morado página 186.

3º jueves 4 de marzo

TRIGONOMETRÍA

Definición: rama de la matemática que estudia las relaciones entre los lados y ángulos de un triángulo.

La trigonometría establece las relaciones entre los lados de un triángulo rectángulo. Ejemplo:

Funciones trigonométricas son las seis posibles combinaciones de los lados del triángulo:

1. Seno de un ángulo agudo: es la razón entre el cateto opuesto y la hipotenusa.
2. Coseno de un ángulo agudo: es la razón entre el cateto adyacente y la hipotenuesa.
3. Tangente de un ángulo agudo: es la razón entre el cateto opuesto y el cateto adyacente.
4. Cotangente de un ángulo agudo: es la razón entre el cateto adyacente y el cateto opuesto.
5. Secante de un ángulo agudo: es la razón entre la hipotenusa y el cateto adyacente.
6. Cosecante de un ángulo agudo: es la razón entre la hipotenusa y el cateto opuesto.

Tarea:

Estudiar las 6 funciones trigonométricas

1º jueves 4 de marzo

Actividad de clase:
Resolver en una fotocopia un ejercicio de identificación de cuadriláteros de acuerdo a su clasificación.
Resolver las páginas 198 y 199 de su libro de la deportista relativo a identificar las características de los cuadriláteros.

CONVERSIONES DE UNIDADES DE LONGITUD

Pegar una fotocopia con un cuadro de unidades de longitud.

1 m = 10 dm

1 m = 100 cm

1 m = 1000 mm

1 m = 0.1 dam

1 m = 0.01 hm

1 m = 0.001 km

Ejemplos:

12 km = 12000 m

30 hm = 30,000 dm

1.45 dam = 14,500 mm

4 dm = 0.04 dam

7000 cm = 70 m

CONVERSIONES DE UNIDADES DE SUPERFICIE.

Pegar una fotocopia con las unidades de superficie:

Ejemplos:

700 km2 = 70,000 hm2

0.4 m2 = 0.004 dam2

1.2 dam2 = 120'000,000 mm2

Tarea:

Resolver las conversiones en su libro de la deportista página 205.

2º jueves 4 de marzo

POLÍGONOS.

Definición de polígonos: figura plana formada por segmentos de rectas llamadas lados del polígono, los puntos de intersección son los vértices del polígono.

Definición de poligonal: serie de segmentos abiertos, es decir que no se unen todos los extremos.

CLASIFICACIÓN DE POLÍGONOS SEGÚN SUS MEDIDAS.

Se clasifican en:

a) Polígonos regulares: todos sus lados son del mismo tamaño.

b) Polígonos irregulares: tienes sus lados de distintos tamaños.

CLASIFICACIÓN DE POLÍGONOS SEGÚN SUS ÁNGULOS.

Se clasifican en:

a) Polígonos convexos: todos sus ángulos son menores de 180º.

b) Polígonos cóncavos: tienen por lo menos un ángulos mayor de 180º.

Diagonal: es una línea que une dos vértices no consecutivos de un polígono.

CLASIFICACIÓN DE POLÍGONOS SEGÚN SUS LADOS.

Tarea:

Trazar todas las diagonales de las figuras de su libro naranja página 186.

3º martes 2 de marzo

Actividad de clase:

Resolverá tres problemas que involucren el teorema de Pitágoras, en su cuaderno:

Ejercicio de clase:

Resolverá los problemas y ejercicios sobre el teorema de Pitágoras en su libro naranja pp. 258 - 262.

Tarea:

Realizar la actividad extra de su libro naranja página 159, relativa a hacer la demostración física con papeles de colores del teorema de Pitágoras.

1º martes 2 de marzo

Actividad de clase:
Trabajar con trazos de cuadriláteros en su libro de la antena páginas 152 - 159. El trabajo será realizado por parejas.

Tarea: No hay tarea

2º martes 2 de marzo

PLANO CARTESIANO:

El plano cartesiano está formado por dos rectas perpendiculares, la recta horizontal llamada eje X o eje de las abscisas, y la recta vertical llamada eje Y o eje de las ordenadas.

En el plano cartesiano ubicamos puntos llamadas coordenadas. Una coordenada está formada por dos números: coordenada : (número de la abscisa, número de la ordenada).

Con el primer número nos movemos a la derecha o a la izquierda, con el segundo número nos movemos hacia arriba o hacia abajo.

Localizar los siguientes puntos en el plano cartesiano:
A (5, 3)
B (-2, 4)
C (-3, -2)
D (3, - 1)
E (0, 3)

El plano cartesiano está dividido en cuatro zonas llamadas cuadrantes:

Actividad de clase:
Resolver ejercicios de relaciones funcionales con su tabla y gráfica en su libro naranja pp. 172 - 182. (El trabajo será por parejas)

Tarea: Ubicar en el plano cartesiano algunos puntos en su libro naranja página183.

3º lunes 1º marzo

SERIES NUMÉRICAS Y FIGURATIVAS.

Actividad de clase:
Resolver las series numéricas y figurativas de su libro morado pp. 177 y 178.
Resolver series numéricas y figurativas en su libro naranja pp. 254 - 257.

2º lunes 1º marzo

RELACIONES FUNCIONALES

Algunas relaciones que son de proporcionalidad directa, no empiezan los valores de inicio con cero, sino que inician con valores diferentes, pero su relación sigue creciendo en forma proporcional, este tipo de relaciones describe una ecuación de la forma:
y = mx + b
donde:
y es el valor a encontrar
x es la variable independiente, puede tener cualquier valor
m es la relación de cambio, o la regla de variación
b es el valor inicial de la relación.

Problema de ejemplo:
1.Para entrar a una escuela tengo que pagar un costo de inscripción de $6,500 y a partir de allí yo pago mensualidades de $4,000.
a) ¿Cuánto dinero habré pagado en 6 meses en total?
Utilizando la función y = mx + b
donde:
y es el valor a encontrar, o sea ¿cuánto dinero?
x es la variable independiente, puede tener cualquier valor, o sea 6 meses
m es la relación de cambio, o la regla de variación, o sea $4,000
b es el valor inicial de la relación, o sea la inscripción $6,500
y = (4,000)(6) + 6,500
y = 24,000 + 6,500
y = 30,500
En 6 meses habré pagado$30,500.

b) ¿Cuánto dinero habré pagado en 10 meses en total?
Utilizando la misma función: y = mx + b
donde:
y es el valor a encontrar, o sea ¿cuánto dinero?
x es la variable independiente, puede tener cualquier valor, o sea 10 meses
m es la relación de cambio, o la regla de variación, o sea $4,000
b es el valor inicial de la relación, o sea la inscripción $6,500
y = (4,000)(10) + 6,500
y = 40,000 + 6,500
y = 46,500
En 10 meses habré pagado$46,500.

c) Si contara con $25,000 ¿para cuántas mensualidades me alcanza?
Utilizo la misma función y = mx + b, donde:
y es el valor a encontrar, o sea ¿cuánto dinero?, en este caso es $25,000
x es la variable independiente, puede tener cualquier valor, o sea x meses
m es la relación de cambio, o la regla de variación, o sea $4,000
b es el valor inicial de la relación, o sea la inscripción $6,500
25,000 = 4,000x + 6500
despejando x:
25,000 – 6,500 = 4,000x
18,500 = 4,000x
18,500/4,000 = x
4.625 = x
Me alcanza para 4.625 mensualidades.

Ejercicio de clase y tarea: resolver los problemas de su libro azul pág. 169.

1º viernes 26 de febrero

CUADRILÁTEROS

Cuadriláteros: son las figuras planas que tienen 4 lados.

PARALELOGRAMOS

Llamamos paralelogramos a las figuras que tienen dos pares de lados paralelos.

Las figuras que son paralelogramos son:

TRAPECIOS

Llamamos trapecios a las figuras que tienen un par de lados paralelos.

Las figuras que son trapecios son:

TRAPEZOIDES

Llamamos trapezoides a las figuras que no tienen lados paralelos.

Tarea: resolver los siguientes problemas para pensar en una hoja para entregar.

3º viernes 26 de febrero

Actividad de clase:
Resolver del libro naranja las página 242, 243 y 247.
Analizar las gráficas no funcionales de su libro morado 166 y 167.

SUCESIONES NUMÉRICAS Y FIGURATIVAS

Definición: una sucesión es una secuencia de números que siguen una regla dada.

TIPOS DE SUCESIONES

• Aritméticas: la regla de la sucesión siempre es el mismo número que se suma o se resta:

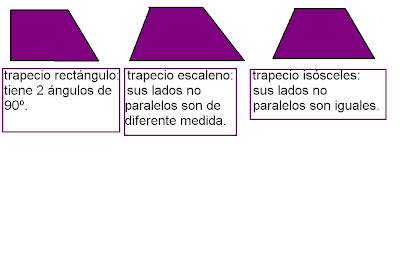
Ejemplo:

2, 5, 8, 11, 14, ... r = +3

• Geométricas: la regla de la sucesión siempre es el mismo número que se multiplica o se divide.

Ejemplo:

72, 36, 18, 9, 4.5, ... r = : 2

• También existen sucesiones de funciones de segundo grado.

Ejemplo: f(x) = x2 + 1

2, 5, 10, 17, ...

REGLAS PARA SUCESIONES ARITMÉTICAS.

Para obtener el número n de una sucesión aritmética, la regla será:

25, 29, 33, 37, 41,... r = +4

a15 = 81

an= (n - 1) (r) + a1

a15 = (14)(4) + 25

a15 = 56 + 25

a15 = 81

Para obtener la suma de los elementos en una sucesión aritmética la regla será:

sn = (a1)(n) + n(n-1)r : 2

s15 = 795

s15 = (25)(15) + (15)(14)(4) : 2

s15 = 375 + 420

s15 = 795

Ejercicio: resolver las sucesiones en su texto morado pp. 175 y 176.

3º jueves 25 de febrero

GRÁFICAS NO FUNCIONALES.

Copiar en su cuaderno las gráficas de su libro naranja página 244 y explicar una situación que dé lugar a cada gráfica realizada.

Resolver las páginas de su libro naranja pp. 244 - 247.

1º jueves 25 de febrero

Actividad de clase:
Trazar y resolver casos de triángulos en su libro de la antena pp. 146 - 151.
Tarea: Trazar y recortar en una hoja de color un cuadrado, un rectángulo, un rombo y un romboide, dadas sus medidas.

2º jueves 25 de febrero

Actividad de clase:

Realizar despejes de fórmulas en su cuaderno. Marcando los errores comunes y que no se deben realizar.

PROBLEMAS QUE DAN LUGAR A SISTEMAS DE ECUACIONES.

1. La suma de dos números es 40 y su diferencia es 6. Hallar los números.


2. La suma de las cifras de un número de dos dígitos es 12 y si al doble de la cifra de las decenas se suman 3 da la cifra de las unidades, ¿cuál es el número?

Ejercicio: Se marcan las parejas de trabajo, por lista, se les asigna algún problema que se refiere a sistemas de ecuaciones y se resuelve.

Tarea: Se pasará dicho problema en un papelote.

3º martes 23 de febrero

FUNCIONES DE SEGUNDO GRADO.

Atender a una presentación sobre cómo se mueve una función de la forma ax2 + bx + c cuando se modifican los valores de a, b y c.

Actividad de clase:
Realizar las funciones de primer grado, segundo grado e hipérbolas en su libro naranja pp. 232 a 243.

Tarea:
Tabular las funciones en su libro naranja pp. 164 y 165.

1º martes 23 de febrero

TRIÁNGULOS

1º CASO: LLL

Dados tres lados de un triángulo sólo es posible trazar un triángulo.

1. Traza en una hoja de color un triángulo de medidas 3cm, 4 cm y 5 cm.

2. Traza en tu cuaderno un triángulo utilizando las mismas medidas.

3. Compara ambos triángulos

2º CASO: LAL

Dados dos lados y un ángulo sólo es posible trazar un triángulo.

1. Traza en una hoja de color un triángulo cuya base mida 6 cm.

2. Mide un ángulo de 60º en un extremo.

3. Alarga el lado del triángulo y marca una línea de 3cm

4. Cierra el triángulo.

5. Traza en tu cuaderno un triángulo utilizando las mismas medidas.

6. Compara ambos triángulos.

3º CASO: ALA

Dado un lado del triángulo y los dos ángulos adyacentes a él, sólo es posible trazar un triángulo.

1. Traza en una hoja de color un triángulo cuya base mida 4 cm.

2. Marca en un extremo un ángulo de 45º y en el otro extremo marca un ángulo de 90º.

3. Alarga los ángulos hasta que se forme un triángulo.

4. Traza en tu cuaderno un triángulo utilizando las mismas medidas.

5. Compara ambos triángulos.

Tarea: Trazar triángulos de los ejercicios simples y de dificultad media en su libro de la deportista pp. 191 a la 195.

2º martes 23 de febrero

Actividad de clase:

Resolver los siguientes sistemas de ecuaciones aplicando el método de sustitución, los dos primeros en su cuaderno, los tres sistemas últimos en hoja para entregar.

5x - 2y = 25
3x + 2y = -1

4x + y = 15
2x - 3y = 11

4x + 4y = 28
2x - 3y = -6

4x - 5y = 6
3x + 2y = -7

5x + y = 10
-4x - 2y = -8

3º lunes 22 de febrero

FUNCIONES DE PRIMER GRADO

Para resolver funciones de primer grado de la forma y = mx + b, donde m es la pendiente (inclinación) y b es el punto donde cruza al eje y.

Ejemplos:

Localizar en el plano cartesiano:

y = 3x - 2

y = -4x + 4

y = 3/5 x + 5

y = -2/7x - 3

Pasos:

1. Se busca el valor de b en el eje y (eje vertical), ése es el primer punto.
2. A partir de él me muevo a la derecha(denominador) y hacia arriba (numerador positivo o abajo (numerador negativo)
3. Trazo la línea.

Nota:
Las funciones que tienen pendiente negativo quedan inclinadas hacia la izquierda. Las funciones que tienen pendiente positiva quedan inclinadas hacia la derecha.

Tarea: Resolver las funciones de su texto morado pp. 162 y 163.

2º lunes 22 de febrero

SISTEMAS DE ECUACIONES CON DOS VARIABLES.

Atender presentación sobre resolver sistemas de ecuaciones por el método de sustitución.

Pasos:

1. Despeje
2. Sustitución
3. Sustitución
4. Comprobación

Ejemplo:

3º viernes 19 de febrero

RELACIONES FUNCIONALES DE 2º GRADO.

Son las que tienen variables con exponente 2.

Una relación funcional de 2º grado marca gráficamente una curva llamada parábola.

RELACIONES FUNCIONALES DE HIPÉRBOLAS.

Son las que tienen en el denominador la x.

Una relación funcional con denominador x gráficamente es una curva llamada hipérbola.

Ejercicio: Resolver las relaciones funcionales y graficarlas en su libro de texto morado pp. 157 - 161.

3º jueves 18 de febrero

RELACIONES FUNCIONALES DE PRIMER GRADO

Son las que la variable tiene exponente uno.

Una relación funcional de primer grado marca gráficamente una línea recta.

Ejercicio: Realizar las funciones y las gráficas en su libro morado pp. 152 a 155.

1º jueves 18 de febrero

PROBLEMAS CON ECUACIONES DE PRIMER GRADO.

Ejemplos:

1. Alfredo y Juan reunieron $840.00 Si Juan aportó el doble que Alfredo, ¿cuánto aportó cada uno?



2. Tres números consecutivos suman 366, ¿qué números son?



3. Hallar un número tal que, disminuido en 56, dé como resultado 124 menos el doble del número buscado.

Resolver ecuaciones de su libro de la deportista página 182.

Tarea: resolver por sorteo un problema de primer grado y pasarlo a papelote.

2º jueves 18 de febrero

DESPEJE DE FÓRMULAS

Definición: es aplicar las propiedades de la igualdad para despejar otra variable de una fórmula.

Ejemplos:

Resolver el ejercicio de su libro azul pp. 162 y 163.

Actividad en hoja para entregar:

resolver un examen de dos ecuaciones:

Tarea:

terminar los despejes de fórmulas de su libro azul.