jueves 26 de noviembre

ECUACIONES.

Pasos para resolver ecuaciones:

1º quitar paréntesis

2º quitar denominadores

3º pasar las x a un solo miembro

4º reducir

5º comprobar

Ejemplos:

Tarea:
Terminar los ejercicios del pase a examen.

1º jueves 26 de noviembre

Actividad de clase:
Resolver problemas y multiplicaciones en su libro de la antena páginas 73, 74, 75, 76.
Tarea:
No hay tarea.

2º jueves 26 de octubre

Resolver los problemas en grupo en el libro naranja:
Página 74 , b)
Actividad 9.3 página 81.
Página 83, e) h) f) i)
Página 84 y 85
Realizar la presentación de trabajos a escala y hacer la votación por los mejores trabajos del grupo.
Realizar el repaso a examen dado en fotocopia.
Tarea:
Terminar el repaso a examen.

3º miércoles 25 de noviembre

TASAS.
Aplicar la fórmula de las tasas para resolver problemas.
Fórmula de la tasa: (dato nuevo - dato anterior) : dato anterior x 100
Ejemplo:
El grupo de 3º tiene 11 alumos, el grupo de 2º tiene 19 alumnos, ¿cuál es la tasa de crecimiento del grupo?
tasa: (19 - 11) : dato anterior x 100
(8) : 11 x 100
tasa: 72.72 % de crecimiento
Resolver los ejercicios de cálculo de tasas y aplicaciones en su texto morado página 85.
Actividad de clase:
Resolver el pase a examen para tercero de secundaria.
Tarea:
Realizar el repaso a examen.

1º martes 24 de noviembre

Actividad de clase:
Realizar los ejercicios y resolver los problemas de su libro de la antena páginas 68 - 71.
Tarea:
Resolver las actividades 3.1 y 3.2 de su libro de la antena página 72.

2º martes 24 de noviembre

Actividad de clase:
Resolver en grupo las páginas 78 - 83.
Presentación sobre el diagrama rectangular y de árbol. Y la elaboración de gráficas.
Tarea:
Realizar por equipos sus cartulinas sobre escalas.

3º lunes 23 de noviembre

Actividad de clase:
Resolver de su libro naranja los problemas y ejercicios sobre arco, sector circular y corona de su libro de texto naranja páginas 82 - 87.
Resolver series aritméticas y geométricas en su libro de texto morado página 86.
Tarea:
Encontrar las coordenadas de su libro de texto naranja páginas 88 y 89.

2º lunes 23 noviembre

Actividad de clase:
Resolver en grupo las páginas del libro naranja 65 - 67.
Resolver por equipos las páginas del libro naranja 68 - 72.
Tarea:
Resolver del libro naranja las páginas 73 - 77.

1º viernes 20 de noviembre

MULTIPLICACIÓN DE FRACCIONES.

¿Cuánto es medio cuarto de jamón?

Medio cuarto se entiende como la mitad de un cuarto:

1/2 de 1/4

Se resuelve numerador por numerador y denominador por denominador.

Ejemplos:

DIVISIÓN DE FRACCIONES.

¿Qué fracción corresponde si divido 1/2 pizza entre 3 personas?

Se resuelve numerador por denominador y denominador por numerador.

Ejemplos:

Ejercicio:

Resolver las operaciones de fracciones en su libro de la antena páginas 60 - 67

Tarea:

Resolver las operaciones con fracciones en su libro de la antena página 69.

3º viernes 20 de noviembre

Actividad de clase:
Corregir y resolver los ejercicios y problemas de su libro de texto naranja páginas 78 - 81.
Presentación tema " Sector circular, arcos y coronas"
De esta presentación hay que pasarlo al cuaderno los conceptos, ejemplos y problema de la cabra. Para enviarles la presentación por correo electrónico, envíenme un mensaje a mi correo que es raquelcaz@yahoo.com.mx y con mucho gusto se los envío.
Tarea:
Resolver en el libro morado las páginas 77 y 78.

3º jueves 19 de noviembre

Actividad de clase:
Resolver los ejercicios de su libro naranja páginas 73 - 77.
Tarea:
Resolver la página 78 de su libro naranja relativo a deducir el valor de ángulos en el círculo.

1º jueves 19 de noviembre

RESTA DE FRACCIONES.

Problema: El día de hoy traía una mochila muy pesada, pesaba 4 3/5 kg, pero al llegar a la escuela, saqué el material que me pidieron para hacer una maqueta. Dicho material pesaba 2 1/2 kg. ¿Cuánto pesa ahora mi mochila?

Ejercicio 1:

Resolver el libro de la antena páginas 58 y 59.

Ejercicio 2:

Resolver el libro de la deportista páginas 103, 104 y 105

Tarea:

Resolver unos cuadrados mágicos con fracciones en su libro de la antena página 58 actividad 1.6

2º jueves 19 de noviembre

Contestar su libro naranja 61-64
Participar en presentación Proporcionalidad múltiple:

Para resolver problemas en los que intervienen tres o más magnitudes se requiere desarrollar la capacidad para interpretar la proporcionalidad múltiple.
Siempre es útil plantear la pregunta:
¿Cómo se puede reducir este problema para una sola persona, objeto o fenómeno?
Ejemplos:

Las experiencias anteriores permiten afirmar que se necesitan 150 litros de agua para una excursión de 12 estudiantes durante 5 días. ¿Cuántos litros de agua se necesitarán para una excursión de 84 estudiantes durante 8 días?
(pienso en reducir los estudiantes y los días, ¿12 estudiantes en 5 días, es igual que _60_ en 1 día?)
(¿84 estudiantes durante 8 días es lo mismo que __672 estudiantes en 1 día?
Ahora el problema lo podemos transformar en 150 litros de agua se necesitan para 60 estudiantes, ¿cuántos litros necesitan 672 estudiantes?

litros estudiantes
150 60
x 672
150 x 672 = 100,800 = 1,680 litros
60 60

Ejemplo 2:

Seis hombres trabajando 8 horas diarias han hecho 192 metros cuadrados de una obra en 12 días. ¿Cuánto tiempo necesitarán 9 hombres trabajando 7 horas diarias para hacer 231 metros de la misma obra?
¿Cómo se puede reducir este problema para una sola persona, objeto o fenómeno?
6 hombres trabajan 8 horas diarias, durante 12 días equivale a 1 hombre trabajando _576__ horas
Esto quiere decir que 192 metros cuadrados se realizaron en 576 horas, ¿cuántas horas se necesitan para realizar 231 metros cuadrados de la misma obra?

metros horas
192 576 231 x 576 = 693
231 x 192

693 horas = 9hombres trabajando 7 horas por x días.
693 = 9 x 7 x _11_
Necesitarán 11 días.

Tarea:
Realizar los trazos a escala y por homotecia en su libro de texto azul páginas 88 y 89.

3º miércoles 18 de noviembre

ÁNGULOS EN EL CÍRCULO

ÁNGULO CENTRAL

Definición: ángulo central es el ángulo cuyo vértice está en el centro del círculo y está formado por dos radios.
Teorema: "Todo ángulo central tiene por medida la misma del arco determinado por sus lados."

ÁNGULO INSCRITO

Definición: ángulo inscrito es el ángulo cuyo vértice está en un punto de la circunferencia y está formado por dos cuerdas.
Teorema: "Todo ángulo inscrito tiene por medida la mitad del arco determinado por sus lados."

Ejercicio: libro naranja 66-73.

Presentación: ángulos en el círculo.

Tarea:

Resolver los ejercicios del libro morado páginas 75 y 76.

1º martes 17 de noviembre

SUMA DE FRACCIONES
Problema: Ayer compramos una pizza grande para cenar: yo me comí 1/4 parte, mi hermano mayor se comió 1/3; llegó mi papá y se comió 3/8; ¿qué fracción le quedó a mi mamá de pizza?
Ejemplos:
Actividades:

1. Actividad 1.4, libro de la antena página 57
2. Actividad 1.3, libro de la antena página 57
3. Actividad 1.1 y 1.2, libro de la antena página 56
4. Libro de la deportista páginas 100 y 102

Tarea:

Resolver los ejercicios complejos del libro de la deportista páginas 100 y 102.

2º martes 17 de noviembre

Pegar figuras recortadas en la clase anterior.
Trazar diagonales para formar triángulos.
Calcular cuánto suman sus ángulos interiores.

Conclusiones:

• La suma de los ángulos de un polígono se obtiene encontrando el número de triángulos en que se pueden dividir.
• Para dividir en triángulos un polígono se trazan las diagonales desde un solo vértice.
• El número de triángulos que se obtiene siempre será el número de lados menos 2.

Ejemplos:

• Un polígono de 10 lados se dividirá en 8 triángulos. La suma de sus ángulos interiores será 8 x 180 = 1440º.
• Un polígono de 20 lados se dividirá en 18 triángulos. La suma de sus ángulos interiores será de 18 x 180 = 3240º.
• Un polígono de 50 lados se dividirá en 48 triángulos. La suma de sus ángulos interiores será de 48 x 180 = 8640º.

Ejercicio. Calcula el valor de los ángulos que faltan.

ESCALAS

Definición: es la representación de un dibujo o figura a una razón dada.

La escala se representa como fracción:

a : b (se lee, a es a b)

a/b

Cuando en la razón de escala el valor de a es mayor que la de b se trata de una ampliación.

Cuando en la razón de escala el valor de a es menor que la de b se trata de una reducción.

Ejercicio:

Traza un cuadrado de 4 cuadritos por lado.

Traza un cuadrado a una escala de 3:2

Traza otro cuadrado a una escala de 1:4

HOMOTECIA

Es la representación a escala utilizando un punto fijo de proyección llamado centro de homotecia.

Pasos para realizar la homotecia:

1. Se trazan líneas del centro de homotecia a los vértices.
2. Si se va a hacer una reducción, por ejemplo: 1:2, se toma la medida de las distancias del centro al vértice y se marca la mitad. Se unen estos puntos y quedará la figura reducida.
3. Si se va a hacer una ampliación, por ejemplo: 2:1, se toma la medida de las distancias del centro al vértice y se marca otro tanto más allá del punto. Se unen estos puntos y quedará la figura ampliada.
   

Tarea:

Traer un dibujo para hacerlos a escala, por equipos, de cada dibujo se traerán 4 copias (una para cada miembro del equipo).

1º viernes 13 de noviembre

FRACCIONES

Simplificación de fracciones: es escribir una fracción equivalente utilizando números de menor valor.

Ejemplos:

TIPOS DE FRACCIONES

• Común: es la fracción cuyo denominador es mayor que el numerador. Siempre representan una porción menor que el entero. Ejemplos:

• Impropia: es la fracción cuyo denominador es menor que el numerador. Siempre representan una porción mayor que el entero. Ejemplos:


• Mixta: es la fracción que está compuesta por un entero y una fracción común. Ejemplos:

CONVERSIONES ENTRE FRACCIONES IMPROPIAS Y MIXTAS

• Convertir una fracción impropia a mixta: se divide. Ejemplos:


• Convertir una fracción mixta a impropia: se multiplica el denominador por el entero y se le suma el numerador, el denominador queda igual. Ejemplos:

Ejercicio:

Libro de la deportista páginas 95, 96, 97 y 98.

Tarea:
Resolver el siguiente problema de lógica:

No se quitaban años, pero hacían lo posible para que no fuese fácil saber sus edades:

Nicolás dice tener el triple de años que Isabel pero dentro de dos años Nicolás sólo doblará la edad de Isabel.
¿Cuántos años tiene cada uno?

3º viernes 13 de noviembre

Trabajo 1:
Libro morado página 73, entre todos y en grupo se resuelve.
Trabajo 2:
Libro naranja páginas 58 - 65. Por equipos.

3º jueves 12 de noviembre

RECTAS NOTABLES DEL CÍRCULO

a) Circunferencia: es el conjunto de puntos que está a la misma distancia de un punto llamado centro.

b) Centro: es el punto fijo que está a la misma distancia de cualquier punto de la circunferencia.

c) Círculo: es la región limitada por una circunferencia.

Segmento: es una porción de línea, tiene principio y fin:

Recta: es una línea que no tiene principio ni fin:

Semirrecta: es una porción de línea, tiene principio y no tiene fin:

RECTAS Y SEGMENTOS DEL CÍRCULO:

1. Radio: es un segmento que va del centro a un punto de la circunferencia. OA


2. Diámetro: es un segmento que une dos puntos de la circunferencia y pasa por el centro. BC


3. Cuerda: es un segmento que une dos puntos de la circunferencia. DE


4. Tangente: es una recta que toca un solo punto de la circunferencia. GF. El punto donde toca a la circunferencia se llama punto de tangencia. (H)


5. Secante: es una recta que corta a la circunferencia en dos puntos diferentes. IJ


6. Recta exterior: es una recta que no toca a la circunferencia en ningún punto. KL


7. Recta normal: es una recta que pasa por el centro de la circunferencia. MN


8. Arco: es un segmento que es porción de una circunferencia. PQ
   

Tarea:
Realizar los trazos de rectas notables en su texto morado páginas 71 y 72.

1º jueves 12 de noviembre

MÁXIMO COMÚN DIVISOR

M.C.D.

Problema: Dos rollos de manguera de 60 metros y 105 metros de longitud respectivamente se van a repartir por igual medida a los trabajadores de Aseo y Limpia. ¿Cuál será la mayor longitud de manguera que recibirá cada empleado y cuántos de ellos resultarán beneficiados?

Ejercicio 1:
Calcular el m. c. d. en su libro de la deportista página 94.

Ejercicio 2:

Resolver problemas en una fotocopia.

Tarea:

Hacer un ejercicio complejo de su libro de la deportista página 94 en una cartulina con cualquier material que no sea de escritura ( no lápiz, no pluma, no color, no plumón, no crayola) puede ser con otro material como plastilina, papel de china enrollado, pasta de sopa, estambre, etc.

2º jueves 12 de noviembre

Actividad de clase:

Resolver las páginas 50 - 60 de su libro naranja.

Actividad 2 de clase:

Recortar los ángulos interiores de tres triángulos y pegarlos en su cuaderno:

Apunte de clase:

ÁNGULOS INTERIORES

"Los ángulos interiores de cualquier triángulo suman 180º."

Tarea:
No hay tarea.

3º miércoles 11 de noviembre

Ejercicio de clase:
A partir de los casos de congruencia, realizar demostraciones en su libro de texto naranja páginas 51 - 53.
Ejercicio 2 de clase:
En equipos de 3 o 4 personas, demostrar los teoremas de su libro de texto naranja páginas 53 y 54.
Tarea:
Investigar las rectas notables del círculo. Incluyendo la fuente de información.

1º martes 10 de noviembre

MÍNIMO COMÚN MÚLTIPLO.

Problema:

Para poner el piso en un pasillo se utilizaron 3 mosaicos de diferente medida. ¿A qué medida mínima coincidirán las hileras con los diferentes mosaicos?

Es un problema de mínimo común múltiplo porque se van a ir sacando los múltiplos de los mosaicos y se verá el número que coinciden las tres hileras.

Actividad 2:

Atender a la presentación de problemas de m.c.m. y m.c.d.

Ejercicio:

Encontrar el m. c. m. de diversos grupos de números en su libro de la deportista página 92.

Tarea:

Calcular el m.c.m. de 24, 36 y 60.

2º martes 10 de noviembre

ÁNGULOS ENTRE PARALELAS.

Repasar los diferentes ángulos entre paralelas resolviendo los ejercicios de su libro de texto naranja páginas 46 - 48.

Atender a una presentación en usos múltiples sobre los ángulos entre paralelas.

Resolver una fotocopia sobre ángulos entre paralelas identificando las parejas de ángulos.

Tarea:

Resolver los ejercicios de ángulos entre paralelas de su texto naranja páginas 49, 56 y 58. Y recortar las figuras geométricas de una fotocopia dada en clase.

2º lunes 9 de noviembre

ÁNGULOS CORRESPONDIENTES.

"Los ángulos correspondientes formados por rectas paralelas son iguales."

ÁNGULOS ALTERNOS INTERNOS.

"Los ángulos alternos internos formados por rectas paralelas son iguales."

ÁNGULOS ALTERNOS EXTERNOS.

"Los ángulos alternos externos formados por rectas paralelas son iguales."

ÁNGULOS COLATERALES INTERNOS.

"Los ángulos colaterales internos formados por rectas paralelas son suplementarios, suman 180º."

ÁNGULOS COLATERALES EXTERNOS.

"Los ángulos colaterales externos formados por rectas paralelas son suplementarios, suman 180º."

Tarea:

Identificar las parejas de ángulos entre rectas paralelas en su texto azul páginas 82 y 83.

1º viernes 6 de noviembre

FACTORIZACIÓN EN PRIMOS.

Encontrar la lista de los primeros 25 números primos resolviendo el ejercicio de su libro de texto de la deportista página 88.

FACTORIZACIÓN EN PRIMOS

Definición de números primos: Son los que tienen sólo 2 divisores: sí mismos y la unidad.

Los 25 primeros números primos son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.

CRITERIOS DE DIVISIBILIDAD

a) Mitad. Son los números que son divisibles por 2.

Terminan en 0, 2, 4, 6 y 8.

b) Tercera. Son los números que son divisibles por 3.

Se suman sus dígitos y el resultado debe ser múltiplo de 3.

c) Quinta. Son los números que son divisibles por 5.

Terminan en 0 y 5.

Ejercicio:

En la siguientes cantidades subraya con rojo las que tienen mitad, con azul las que tienen tercera y con negro las que tienen quinta:

Factoriza en primos los números:

Ejercicio:

Factorizar los números de su libro de texto de la deportista página 89 y 90.

Tarea:

Factorizar los números en una hoja de block: 72, 900, 2970, 513 y 650.

3º viernes 6 de noviembre

CASOS DE CONGRUENCIA

Llamamos triángulos congruentes a las que son iguales. El símbolo de congruencia es:

Los triángulos congruentes tienen las mismas medidas de ángulos y de lados.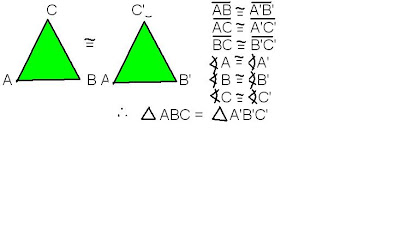

Ejemplo:

Llamamos casos de congruencia a los requisitos mínimos que deben tener 2 triángulos para que sean congruentes.

Los casos de congruencia son tres: LLL, LAL y ALA.

CASO DE CONGRUENCIA LLL

Dos triángulos son congruentes cuando tienen igual sus tres lados. (LLL)

CASO DE CONGRUENCIA LAL

Dos triángulos son congruentes cuando tienen igual dos lados y el ángulo comprendido entre ellos. (LAL)

CASOS DE CONGRUENCIA ALA

Dos triángulos son congruentes cuando tienen igual dos ángulos y el lado comprendido entre ellos. (ALA)

CASOS NO CONGRUENTES.

a) Dos triángulos no son congruentes si tienen iguales sus tres ángulos.

b) Dos triángulos no son congruentes si tienen iguales dos lados y un ángulo, no comprendido entre ellos.

Tarea:

Encontrar si dos triángulos son congruentes o no, y si lo son definir cuál caso de congruencia se cumple en su libro morado páginas 69 y 70.

1º jueves 5 de noviembre

PROBLEMAS CON NÚMEROS DECIMALES.

Resolver los problemas de su libro de texto de la antena páginas 62 a la 64.

APUNTE EN EL CUADERNO:

SUMAS Y RESTAS DE DECIMALES

a) Para la suma de números decimales, se acomodan las cantidades alineando el punto decimal.

Ejemplo:

136.12 + 4.768 + 15 =

b) Para restar números decimales, se acomodan las cantidades alineando el punto decimal, y rellenando con ceros cuando sea necesario.

Ejemplo:

Restar 136.25 - 3.984 =

Tarea:

Investigar los criterios de divisibilidad para sacar mitad, tercera y quinta.

2º jueves 5 de noviembre

PARES DE RECTAS

Las rectas pueden ser:

ÁNGULOS ADYACENTES

Definición: Son los ángulos que comparten un lado y un vértice, esntán uno al lado del otro.

En rectas oblicuas los ángulos adyacentes suman 180º, es decir son suplementarios.

Ejemplos:

ÁNGULOS OPUESTOS POR EL VÉRTICE

Definición: Son los ángulos que tienen el mismo vértice y quedan uno frente al otro.

En rectas oblicuas los ángulos opuestos por el vértice son iguales.

Ejemplos:

Presentación en usos múltiples: Resolución de problemas donde intervienen ángulos.

Tarea:

Terminar los problemas de su libro naranja página 41 y trazar en hojas de papel de china cinco pares de rectas paralelas, separadas aproximadamente 3 centímetros y cruzadas por una transversal.

3º miércoles 4 de noviembre

SUMA Y DIFERENCIA DE CUBOS:

X3 + Y3

X3 - Y3

Ejemplos:

Características:

- Son 2 términos.

- Son cubos perfectos. (tienen raíz cúbica exacta)

Pasos:

1. Sacar raíz cúbica de los dos términos y ponerlos en un paréntesis con sus mismos signos.
2. Cuadrado de la raíz cúbica del primer término, cambiar el signo del segundo término, multiplicación de las dos raíces cúbicas, más, cuadrado de la raíz cúbica del segundo término.

Ejercicio en el cuaderno:

Ejercicio en el libro morado:

Páginas 59 y 60.

Ejercicio en la ficha:

Completar los dos últimos casos de factorización en su ficha bibliográfica.

Ejercicio de factorización:

Resolver en fotocopia un ejercicio para identificar y resolver todos los casos vistos de factorización.

Tarea:

Forrar o enmicar las fichas de factorización y traer juego de geometría completo.