1º viernes 26 de febrero

CUADRILÁTEROS

Cuadriláteros: son las figuras planas que tienen 4 lados.

PARALELOGRAMOS

Llamamos paralelogramos a las figuras que tienen dos pares de lados paralelos.

Las figuras que son paralelogramos son:

TRAPECIOS

Llamamos trapecios a las figuras que tienen un par de lados paralelos.

Las figuras que son trapecios son:

TRAPEZOIDES

Llamamos trapezoides a las figuras que no tienen lados paralelos.

Tarea: resolver los siguientes problemas para pensar en una hoja para entregar.

3º viernes 26 de febrero

Actividad de clase:
Resolver del libro naranja las página 242, 243 y 247.
Analizar las gráficas no funcionales de su libro morado 166 y 167.

SUCESIONES NUMÉRICAS Y FIGURATIVAS

Definición: una sucesión es una secuencia de números que siguen una regla dada.

TIPOS DE SUCESIONES

• Aritméticas: la regla de la sucesión siempre es el mismo número que se suma o se resta:

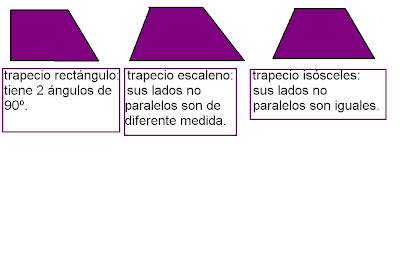
Ejemplo:

2, 5, 8, 11, 14, ... r = +3

• Geométricas: la regla de la sucesión siempre es el mismo número que se multiplica o se divide.

Ejemplo:

72, 36, 18, 9, 4.5, ... r = : 2

• También existen sucesiones de funciones de segundo grado.

Ejemplo: f(x) = x2 + 1

2, 5, 10, 17, ...

REGLAS PARA SUCESIONES ARITMÉTICAS.

Para obtener el número n de una sucesión aritmética, la regla será:

25, 29, 33, 37, 41,... r = +4

a15 = 81

an= (n - 1) (r) + a1

a15 = (14)(4) + 25

a15 = 56 + 25

a15 = 81

Para obtener la suma de los elementos en una sucesión aritmética la regla será:

sn = (a1)(n) + n(n-1)r : 2

s15 = 795

s15 = (25)(15) + (15)(14)(4) : 2

s15 = 375 + 420

s15 = 795

Ejercicio: resolver las sucesiones en su texto morado pp. 175 y 176.

3º jueves 25 de febrero

GRÁFICAS NO FUNCIONALES.

Copiar en su cuaderno las gráficas de su libro naranja página 244 y explicar una situación que dé lugar a cada gráfica realizada.

Resolver las páginas de su libro naranja pp. 244 - 247.

1º jueves 25 de febrero

Actividad de clase:
Trazar y resolver casos de triángulos en su libro de la antena pp. 146 - 151.
Tarea: Trazar y recortar en una hoja de color un cuadrado, un rectángulo, un rombo y un romboide, dadas sus medidas.

2º jueves 25 de febrero

Actividad de clase:

Realizar despejes de fórmulas en su cuaderno. Marcando los errores comunes y que no se deben realizar.

PROBLEMAS QUE DAN LUGAR A SISTEMAS DE ECUACIONES.

1. La suma de dos números es 40 y su diferencia es 6. Hallar los números.


2. La suma de las cifras de un número de dos dígitos es 12 y si al doble de la cifra de las decenas se suman 3 da la cifra de las unidades, ¿cuál es el número?

Ejercicio: Se marcan las parejas de trabajo, por lista, se les asigna algún problema que se refiere a sistemas de ecuaciones y se resuelve.

Tarea: Se pasará dicho problema en un papelote.

3º martes 23 de febrero

FUNCIONES DE SEGUNDO GRADO.

Atender a una presentación sobre cómo se mueve una función de la forma ax2 + bx + c cuando se modifican los valores de a, b y c.

Actividad de clase:
Realizar las funciones de primer grado, segundo grado e hipérbolas en su libro naranja pp. 232 a 243.

Tarea:
Tabular las funciones en su libro naranja pp. 164 y 165.

1º martes 23 de febrero

TRIÁNGULOS

1º CASO: LLL

Dados tres lados de un triángulo sólo es posible trazar un triángulo.

1. Traza en una hoja de color un triángulo de medidas 3cm, 4 cm y 5 cm.

2. Traza en tu cuaderno un triángulo utilizando las mismas medidas.

3. Compara ambos triángulos

2º CASO: LAL

Dados dos lados y un ángulo sólo es posible trazar un triángulo.

1. Traza en una hoja de color un triángulo cuya base mida 6 cm.

2. Mide un ángulo de 60º en un extremo.

3. Alarga el lado del triángulo y marca una línea de 3cm

4. Cierra el triángulo.

5. Traza en tu cuaderno un triángulo utilizando las mismas medidas.

6. Compara ambos triángulos.

3º CASO: ALA

Dado un lado del triángulo y los dos ángulos adyacentes a él, sólo es posible trazar un triángulo.

1. Traza en una hoja de color un triángulo cuya base mida 4 cm.

2. Marca en un extremo un ángulo de 45º y en el otro extremo marca un ángulo de 90º.

3. Alarga los ángulos hasta que se forme un triángulo.

4. Traza en tu cuaderno un triángulo utilizando las mismas medidas.

5. Compara ambos triángulos.

Tarea: Trazar triángulos de los ejercicios simples y de dificultad media en su libro de la deportista pp. 191 a la 195.

2º martes 23 de febrero

Actividad de clase:

Resolver los siguientes sistemas de ecuaciones aplicando el método de sustitución, los dos primeros en su cuaderno, los tres sistemas últimos en hoja para entregar.

5x - 2y = 25
3x + 2y = -1

4x + y = 15
2x - 3y = 11

4x + 4y = 28
2x - 3y = -6

4x - 5y = 6
3x + 2y = -7

5x + y = 10
-4x - 2y = -8

3º lunes 22 de febrero

FUNCIONES DE PRIMER GRADO

Para resolver funciones de primer grado de la forma y = mx + b, donde m es la pendiente (inclinación) y b es el punto donde cruza al eje y.

Ejemplos:

Localizar en el plano cartesiano:

y = 3x - 2

y = -4x + 4

y = 3/5 x + 5

y = -2/7x - 3

Pasos:

1. Se busca el valor de b en el eje y (eje vertical), ése es el primer punto.
2. A partir de él me muevo a la derecha(denominador) y hacia arriba (numerador positivo o abajo (numerador negativo)
3. Trazo la línea.

Nota:
Las funciones que tienen pendiente negativo quedan inclinadas hacia la izquierda. Las funciones que tienen pendiente positiva quedan inclinadas hacia la derecha.

Tarea: Resolver las funciones de su texto morado pp. 162 y 163.

2º lunes 22 de febrero

SISTEMAS DE ECUACIONES CON DOS VARIABLES.

Atender presentación sobre resolver sistemas de ecuaciones por el método de sustitución.

Pasos:

1. Despeje
2. Sustitución
3. Sustitución
4. Comprobación

Ejemplo:

3º viernes 19 de febrero

RELACIONES FUNCIONALES DE 2º GRADO.

Son las que tienen variables con exponente 2.

Una relación funcional de 2º grado marca gráficamente una curva llamada parábola.

RELACIONES FUNCIONALES DE HIPÉRBOLAS.

Son las que tienen en el denominador la x.

Una relación funcional con denominador x gráficamente es una curva llamada hipérbola.

Ejercicio: Resolver las relaciones funcionales y graficarlas en su libro de texto morado pp. 157 - 161.

3º jueves 18 de febrero

RELACIONES FUNCIONALES DE PRIMER GRADO

Son las que la variable tiene exponente uno.

Una relación funcional de primer grado marca gráficamente una línea recta.

Ejercicio: Realizar las funciones y las gráficas en su libro morado pp. 152 a 155.

1º jueves 18 de febrero

PROBLEMAS CON ECUACIONES DE PRIMER GRADO.

Ejemplos:

1. Alfredo y Juan reunieron $840.00 Si Juan aportó el doble que Alfredo, ¿cuánto aportó cada uno?



2. Tres números consecutivos suman 366, ¿qué números son?



3. Hallar un número tal que, disminuido en 56, dé como resultado 124 menos el doble del número buscado.

Resolver ecuaciones de su libro de la deportista página 182.

Tarea: resolver por sorteo un problema de primer grado y pasarlo a papelote.

2º jueves 18 de febrero

DESPEJE DE FÓRMULAS

Definición: es aplicar las propiedades de la igualdad para despejar otra variable de una fórmula.

Ejemplos:

Resolver el ejercicio de su libro azul pp. 162 y 163.

Actividad en hoja para entregar:

resolver un examen de dos ecuaciones:

Tarea:

terminar los despejes de fórmulas de su libro azul.

3º martes 16 de febrero

HOMOTECIA

Definición: nos permite trazar figuras semejantes utilizando rectas que tienen un punto en común llamado centro de homotecia.

Atender a una presentación sobre homotecia escribiendo los conceptos principales.
Resolver por homotecia los ejercicios en su libro naranja pp. 224 - 230

Tarea:
Resolver por homotecia las páginas 148 y 149.

1º martes 16 de febrero

ECUACIONES CON SIMPLIFICACIÓN

Ejemplos:

Pasos:

1. Encierro los elementos desacomodados: primer miembro los elementos que no tienen x y en el segundo miembro los elementos que sí tienen x
2. Escribo nuevamente la ecuación y los términos encerrados se escribe su inverso o simétrico en ambos miembros para que no se afecte la igualdad.
3. Se reduce
4. Se divide

Tarea:Resolver las ecuaciones 1 y 2 de su texto de la deportista página 180.

2º martes 16 de febrero

Actividad de clase:

Repartir por sorteo el problema que les toque de su libro naranja pp. 168 y 169 y de su libro azul pág. 160.

Resolver el problema, pasarlo a papelote.

Exponer el problema al grupo.

Tarea:

Resolver en hoja para entregar las ecuaciones:

3º lunes 15 de febrero

TEMARIO BLOQUE IV

1. Homotecia
2. Relaciones funcionales de primer grado, segundo grado e hipérbola
3. Gráficas no funcionales
4. Sucesiones numéricas y figurativas
5. Problemas con el teorema de Pitágoras
6. Funciones trigonométricas
7. Círculo unitario
8. Triángulo rectángulo
9. Crecimiento aritmético y geométrico
10. Problemas con ecuaciones de primer grado, segundo grado y sistemas
11. Deducción de funciones
12. Cónicas y cilindros
13. Cortes a cuerpos geométricos
14. Volúmenes de cuerpos geométricos

2º lunes 15 de febrero

ECUACIONES CON DENOMINADORES

Pasos:

1. Busco el común denominador o mínimo común múltiplo y toda la ecuación se multiplica por dicho número.
2. Se encierran los términos desacomodados:

a) primer miembro: no tienen x

b) segundo miembro: sí tienen x

3. Se cambian estos términos de miembro y también de signo.

4. Se reduce.

Actividad de clase:

Pasar al pizarrón y resolver las ecuaciones de su libro naranja páginas 167, 169 y 170.

Tarea:

Realizar la actividad extra de su libro naranja página 170

1º viernes 12 de febrero

TEMARIO BIMESTRE IV

1. Ecuaciones de primer grado
2. Triángulos
3. Casos de congruencia
4. Cuadriláteros
5. Conversiones de unidades de medida
6. Áreas y perímetrosde triángulos y cuadriláteros
7. Relaciones de proporcionalidad
8. Porcentajes
9. Tablas de frecuencia
10. Gráficas
11. Probabilidad
12. Números con signo
13. Potenciación y radicación
14. Relaciones funcionales
15. Rectas y segmentos del círculo
16. Fórmulas del círculo
17. Fórmulas de polígonos

ECUACIONES DE PRIMER GRADO

Encontrar el valor de la incógnita para que la operación resulte verdadera:

Tarea:Resolver los ejercicios simples de su libro de texto de la deportista página 180.

2º jueves 11 de febrero

ECUACIONES CON PARÉNTESIS.

Pasos:

1.Quitar los paréntesis:

a) + ( ) se pasa igual.

b) - ( ) se cambian signos

c) número( ) se multiplica.

2. Se encierrarn los términos que no tienen x en el primer miembro y los que sí tienen x en el 2º miembro.

3. se cambian de miembro los términos encerrados, cuidando de cambiar también de signo

4. Se reduce.

Ejemplos:

Ejercicio:

Resolver del libro azul las ecuaciones 1 y 2 de las páginas 158 y 159.

3º martes 9 de febrero

TEOREMA DE TALES

"Si dos o más paralelas determinan segmentos proporcionales en alguna transversal que las cruce, determinan segmentos proporcionales en cualquier otra transversal que cruce las paralelas."

TRAZO DE SEGMENTOS IGUALES CON COMPÁS Y ESCUADRAS.
1) Divide AB en 4 partes iguales:
2) Divide AB en 7 partes iguales:
Pasos:
1º Traza una línea inclinada a partir de A.
2º Se divide con el compás en n partes iguales.
3º Se une la última marca con B.
4º Se trazan paralelas.

TRAZO DE SEGMENTOS A UNA RAZÓN DADA CON COMPÁS Y ESCUADRAS.
1) Divide AB a razón de 3 es a 5:
2) Divide AB a razón de 1 es a 3:
Pasos:
1º Se traza una línea inclinada a partir de A.
2º Se suman las partes de la razón y se divide esta línea en ese número de partes.
3º Se une la última marca con B.
4º Se traza una línea paralela donde marque el primer número de la razón.

TRAZO DE CUARTA PROPORCIONAL CON COMPÁS Y ESCUADRAS.
1) Traza la cuarta proporcional de:
Pasos:
1º Se traza una línea horizontal cualquiera, en ella se marcan con el compás las medidas de a y b
2º Se traza una línea inclinad, en ella se marca con el compás la medida de c.
3º Se une a y c.
4º Se traza una línea paralela con la marca de b.

1º martes 9 de febrero

Actividad 1 de clase: terminar los ejercicios de lenguaje algebraico en su libro de la deportista pp. 177 y 178.

ECUACIONES DE PRIMER GRADO

Resolver las siguientes adivinanzas:

1. Hallar un número que sumado a 90 nos dé 100. x + 90 = 100 x = 10
2. Hallar un número que sumado a 3 nos dé 50. x + 3 = 50 x = 47
3. Hallar un número que restado a 20 nos dé 15. 20 - x = 15 x = 5
4. Hallar un número que restado a 100 nos dé 1. 100 - x = 1 x = 99
5. Hallar un número que al restarle 3 nos dé 25. x - 3 = 25 x = 28
6. Hallar un número que al restarle 15 nos dé 4. x - 15 = 4 x = 19
7. Hallar un número que al multiplicarlo por 5 nos dé 100. 5x = 100 x = 20
8. Hallar un número que al multiplicarlo por 15 nos dé 225. 15x = 225 x = 15
9. Hallar un número que al dividirlo entre 5 nos dé 4. x/5 = 4 x = 20
10. Hallar un número que al dividirlo entre 10 nos dé 50. x/10 = 50 x = 500
11. Hallar un número al que se divide 80 para que nos dé 2. 80/x = 2 x = 40
12. Hallar un número al que se divide 42 para que nos dé 6. 42/x = 6 x = 7

PROPIEDAD FUNDAMENTAL DE LA IGUALDAD.

Si a un miembro de la igualdad le sumamos un número, al segundo miembro de la igualdad le debemos sumar el mismo número.

Ecuación: Es una igualdad que tiene incógnitas.

Resolver una ecuación: es encontrar el valor de la incógnita, a este resultado le llamamos raíz de la ecuación.

Partes de la ecuación:

Ejercicio de clase: Resolver las páginas 136 y 137 de su libro de la antena.

2º martes 9 de febrero

TEMARIO BIMESTRE IV.

1. Ecuaciones con paréntesis
2. Ecuaciones con denominadores
3. Despeje de fórmulas
4. Sistemas de ecuaciones por método de sustitución
5. Relación funcional
6. Ángulos interiores
7. Fórmulas de diagonales en polígonos
8. Polígonos regulares
9. Plano cartesiano
10. Recubrimiento del plano
11. Teselación
12. Funciones
13. Gráficas y = mx + b
14. Leyes de los exponentes
15. Notación científica
16. Criterios de congruencia

3º lunes 8 de febrero

DISCRIMINANTE

Definición: el discriminante es un número que forma parate de la fórmula general:

b2 -4ac

Se pueden dar tres casos:

a) Discriminante es un número positivo: en este caso la ecuación tendrá dos resultados reales.

Gráficamente:

b) Discriminante es 0: en este caso la ecuación tendrá un solo resultado real, o bien sus dos resultados son iguales.

Gráficamente:

c) Discriminante es un número negativo: en este caso la ecuación tendrá dos resultados imaginarios, es decir, no son reales.

Gráficamente:

3º viernes 5 de febrero

FÓRMULA GENERAL PARA ECUACIONES INCOMPLETAS.

Fórmula general:

Incompleta pura:

Incompleta mixta:

Ejercicio de clase: Libro naranja pp. 206 - 208

1º jueves 4 de febrero

REDUCCIÓN DE MULTIPLICACIONES

Ejemplos:

Ley de los exponentes: en las multiplicaciones los exponentes se suman.

Ejercicio:

Resolver en su libro de la deportista las páginas 173, 174 y 175.

Actividad de clase:

Resolver los ejercicios de su repaso a examen correspondiente al bloque III.

2º jueves 4 de febrero

Actividad de clase:

• Resolver las ecuaciones de primer grado en su libro naranja páginas 161 - 164.
• Resolver las ecuaciones de primer grado en su libro azul páginas 156 y 157
• Resolver los ejercicios de repaso a examen correspondiente al bloque III.

Ecuaciones resueltas en su cuaderno en clase:

Tarea:

Resolver el repaso a examen para el próximo lunes 8 de febrero.

3º martes 2 de febrero

RESOLUCIÓN DE ECUACIONES DE 2º GRADO POR FÓRMULA GENERAL

La fórmula general es:

Pasos:

1º Sustituir los valores de a, b y c

2º efectuar el cuadrado y las multiplicaciones

3º restar ( o sumar)

4º sacar raíz

5º separar y reducir

Ejemplo:

4x2 - 25x - 111 = 0

Ejercicio:

Aplicar la fórmula general para resolver las ecuaciones en su cuaderno:

7x2 + x - 5 = 0

-2x2 + 3x - 1 = 0

Ejercicio:

Resolver las ecuaciones por fórmula general en su texto morado páginas 140 y 141.

Tarea:

Resolver los problemas de su texto morado páginas 141 y 142.

1º martes 2 de febrero

Actividad:

Unir a manera de juego de tripas de gato los términos semejantes escritos en el pizarrón.

TÉRMINOS SEMEJANTES

Definición de términos algebraico. Es una expresión formada por un coeficiente y una parte literal.

Ejemplo:

Definición de términos semejantes: Son los que tienen la misma parte literal y diferente coeficiente.

Escribe términos semejantes a:

+4m4n

-15t3

+m

REDUCCIÓN DE TÉRMINOS SEMEJANTES EN SUMAS

Ejemplos:

m + m + m + m = 4m

3x + 4x + 6x + x = 14x

a + a + b + b + a + a + b= 4a + 3b

7m - 5p + 2m - 3p + 6m + p = 15m - 7p

Ley de los signos:

Signos iguales se suman, signos diferentes se restan y queda el signo de mayor valor absoluto.

Ejercicio:

Reducir términos semejantes en sumas en su texto de la deportista páginas 169 y 170

Tarea:

Reducir términos semejantes en sumas en su texto de la deportista páginas 171 y 172.

2º martes 2 de febrero

Actividad de clase:

Resolver del libro naranja los ejercicios páginas 156 - 159.

ECUACIONES DE PRIMER GRADO.

Definición de ecuación: es una igualdad entre dos expresiones algebraicas

Resolver una ecuación: es encontrar el valor de la incógnita que hace verdadera una igualdad, a este valor se le conoce como raíz de la ecuación.

Partes de la ecuación:

Pasos para resolver una ecuación:

1º Los términos con literal se acomodan en el primer miembro y los términos sin literal se acomodan en el segundo miembro. Para cambiar un término de miembro se cambia la operación: si está sumando se pasa restando y si está restando se pasa sumando.

2º Se despeja diviendo el número del segundo miembro entre el que acompaña a la incógnita. (no se cambia de signo)

3º Dividimos

4º Comprobamos.

Tarea: resolver de su libro naranja las páginas 159 y 160.

3º jueves 28 de enero

Ejercicio de clase:
Resolver los ejercicios de su libro de texto naranja páginas 203 y 204.

1º jueves 28 de enero

JERARQUÍA DE OPERACIONES.




Definición de jerarquía: es el orden en que se realizan las operaciones.


1º potencias y raíces
2º multiplicaciones y divisiones
3º sumas y restas


Resolver aplicando la jerarquía las siguientes operaciones:

Ejercicio:

Resolver aplicando la jerarquía de operaciones los ejercicios simples y de dificultad media de su libro de la deportista páginas 167 y 168.

2º jueves 28 de enero

SERIES

Definición de serie: es una sucesión de números que sigue una regla dad.

Serie aritmética: es aquella donde se repite el mismo número ya sea sumado o restado en la sucesión.

Para encontrar el elemento n en una sucesión la regla es:

Ejercicio:

Resolver las series de su libro de texto azul página 154.

Ejercicio:

Resolver series en una página de internet, en el salón de cómputo. Una vez encontrada la serie, escribirla completa en una hoja para entregar.

Tarea:

Terminar las series de su libro azul página 154.